关于相机内参与外参的浅读
学习人脸3D重建的第一天,在首次接触3D相关的内容,必须要搞清楚相机的成像原理,如何将真实三维空间中的三维点与显示器、屏幕和图像等二维成像的平面映射,以及了解该过程的推导方式和相关坐标系的换算,如像素坐标,图像坐标,相机坐标以及世界坐标这四种关系的变换。 主要内容从以下博主的文章整理,并结合自己的实验代码进行测试,推荐直接看原帖,无中间商赚差价:
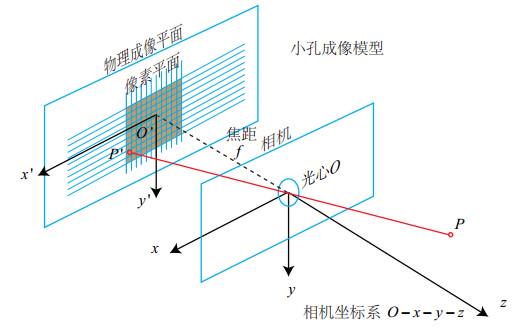
针孔模型
从图中所示,我们可以清楚的看到两种坐标系:
- 相机坐标系(3D):以光心中心点\(O\)为原点,建立\(O-X-Y-Z\)三维坐标系;
- 图像坐标系(2D):以被投射的平面中\(O^{'}\)为原点,建立\(O^{'}-X^{'}-Y^{'}\)二维坐标系。
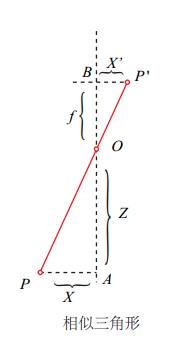
从图所示,取真实世界中的任意一点$P$通过相机的光心$O$点映射到成像平面上的点\(P^{'}\),其中我们令点\(P=\left[\begin{array}{c} x \\ y \\ z \end{array}\right]\),则对应到点\(P^{'}=\left[\begin{array}{c} x^{'} \\ y^{'} \\ z^{'} \end{array}\right]\),这边比较特殊,将成像的平面与光点的距离记为f,即为像距,所以可以用以下图表示坐标系和映射点之间的关系:
通过上图相似三角形关系可以得出以下关系式: \(\frac{z}{f}=-\frac{x}{x^{'}}=-\frac{y}{y^{'}}\) 其中出现负号的原因是因为坐标轴在映射过程中的成像为倒立所导致,为了表达方便,看到一个博主是这样解释和处理的: 为了表示起来更方便,我们把成像平面从相机的后面对称到前面去,这样,负号就没有了。
经过转换后的关系: \(\frac{z}{f}=\frac{x}{x^{'}}=\frac{y}{y^{'}}\) 通现在我们把上面的关系式以解出$P^{‘}$点为目的进行变形,可得: \(x^{'}=f·\frac{x}{z}\),\(y^{'}=f·\frac{y}{z}\) 上面便是整理好的小孔模型基本公式,通过这些公式我们可以进一步的去推算利用该模型下求解相机的内参和外参。
相机内参
简单的描述一下相机内参:相机内参描述了相机本身自带的一些属性,如焦距、像素间距等;通常是用一个内参矩阵K来表示,这个矩阵K用于描述从三维场景到二维场景的映射形状和大小。 上一步我们求解出了小孔模型的基本公式,需要进一步将所述的坐标点映射到像素坐标系中,像素坐标定义通常如下:
- 像素坐标系(2D):通常以图像的左上角为坐标的原点,u轴从左到右与x轴平行,v轴从上到下与y轴平行; 我们设像素坐标轴同时在u轴和v轴缩放了S的倍数,倍数定义为\(S=\left[\begin{array}{c} α \\ β \end{array}\right]\),即u轴缩放了α倍,v轴缩放了β倍;同时,原点坐标也平移了C个像素点,即\(C=\left[\begin{array}{c} c_x \\ c_y \end{array}\right]\),在与上一步求解的点\(P^{'}\)的坐标关系如下:
将上一步以$P^{‘}$与$P$关系得出的小孔模型公式代入可得:
\[u=α·f·\frac{x}{z} +c_x\] \[v=β·f·\frac{y}{z} +c_y\]我们令\(f_x=α·f\),\(f_y=β·f\),可得:
\[u=f_x·\frac{x}{z} +c_x\] \[v=f_y·\frac{y}{z} +c_y\]我们将方程组写成齐次坐标的形式:
\[\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right] = \frac{1}{z}·\left[\begin{array}{c} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{array}\right]·\left[\begin{array}{c} x \\ y \\ z \end{array}\right]\]我们可以把z挪到左边得到:
\[z·\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right] = \left[\begin{array}{c} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{array}\right]·\left[\begin{array}{c} x \\ y \\ z \end{array}\right]\]并且,令\(K=\left[\begin{array}{c} f_x & 0 & c_x \\ 0 & f_y & c_y \\ 0 & 0 & 1 \end{array}\right]\),\(P=\left[\begin{array}{c} x \\ y \\ z \end{array}\right]\),\(P_{uv}=\left[\begin{array}{c} u \\ v \\ 1 \end{array}\right]\),
可得简化的表达式:\(zP_{uv}=KP\) 通过上面的推导,我们已经计算出了相机内参(Camera Intrinsics)的内参矩阵K,通常在实际项目中该内参的得出方式通常需要标定,标定的方式后面等到具体实践再进行整理。
相机外参
简单的描述一下相机的外参:相机的外参主要描述的是相机在三维场景下的位置以及镜头朝向,通常以一个旋转矩阵R和平移向量t进行表示,描述了相机的位置、方向和观察角度,决定了相机从哪个角度观察场景。 在上面的推导过程中,我们已经求出了坐标系之间的关系以及内参矩阵,其中内参矩阵是通过相机坐标系与像素坐标之间的关系得出,所以我们这步需要通过世界坐标系与相机坐标系之间的关系来推导相机外参,并记录过程。 根据上面描述的内容,我们继续以上述为例,设\(P\)是在相机坐标系的点,\(P_w\)是在世界坐标系下的点,我们可以使用一个旋转矩阵\(R\)和一个平移向量\(t\),把\(P\)变换到\(P_w\),即:
\[P=RP_w+t\]其中,\(R\)是一个3x3的旋转矩阵,\(t\)是一个3x1的平移向量,我们将其使用其次坐标表达:
\[\left[\begin{array}{c} x_c \\ y_c \\ z_c \end{array}\right] = \left[\begin{array}{c} R_{11} & R_{12} & R_{13} \\ R_{21} & R_{22} & R_{23} \\ R_{31} & R_{32} & R_{33} \end{array}\right] · \left[\begin{array}{c} x_w \\ y_w \\ z_w \end{array}\right] + \left[\begin{array}{c} t_1 \\ t_2 \\ t_3 \end{array}\right]\]可以改变式子,把加号也干掉:
\[\left[\begin{array}{c} x_c \\ y_c \\ z_c \\ 1 \end{array}\right] = \left[\begin{array}{c} R_{11} & R_{12} & R_{13} & t_1 \\ R_{21} & R_{22} & R_{23} & t_2 \\ R_{31} & R_{32} & R_{33} & t_3 \\ 0 & 0 & 0 & 1 \end{array}\right] · \left[\begin{array}{c} x_w \\ y_w \\ z_w \\ 1 \end{array}\right]\]所以将旋转矩阵$R$和平移向量$t$带入到上述公式可得:
\[\left[\begin{array}{c} x_c \\ y_c \\ z_c \\ 1 \end{array}\right] = \left[\begin{array}{c} R & t \\ 0^T & 1 \end{array}\right] · \left[\begin{array}{c} x_w \\ y_w \\ z_w \\ 1 \end{array}\right]\]所以我们可以使用该矩阵来表示相机的外参:
\[\left[\begin{array}{c} R & t \\ 0^T & 1 \end{array}\right]\]内参与外参组合使用
由于上述内容可得知:
- 相机外参公式:\(P=RP_w+t\)
- 相机内参公式:\(zP_{uv}=KP\)
- 则将外参公式带入内参可得:\(zP_{uv}=K(RP_{W}+t)\)
代码示例
完成上述公式的推导后,使用Python环境下进行实际操作一下,仅使用numpy的ndarray作为数据结构和opencv的绘图工具以及solvePnP来验证相机外参解法。
示例1:模拟与可视化结果
首先我们需要先定义一个被观测的目标,并将其定义在世界坐标中;这里我们就选择使用一个立方体作为观测目标:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
import cv2
import numpy as np
# 定义方形画布像素坐标长度
canvas_square_size = 320
# 定义立方体的边长
length = 1
# 定义立方体的8个顶点坐标 使用世界坐标作为表达
vertices_w = np.array([
[-length / 2, -length / 2, -length / 2],
[-length / 2, -length / 2, length / 2],
[-length / 2, length / 2, -length / 2],
[-length / 2, length / 2, length / 2],
[length / 2, -length / 2, -length / 2],
[length / 2, -length / 2, length / 2],
[length / 2, length / 2, -length / 2],
[length / 2, length / 2, length / 2]])
print("像素坐标系顶点集合: ", vertices_uv.shape)
# 打印结果:
# 世界坐标系顶点集合: (8, 3)
定义好世界坐标下的立方体后,我们来手动定义一组相机外参,上述提到过,相机外参是由一个旋转矩阵R和一个平移向量t组成,这里我们利用旋转矩阵的特性,定义一个携带让其沿着roll轴旋转一定角度的RulerAngle属性的旋转矩阵R_roll,并手动设置一个t向量;使用世界坐标系对其进行变换得出相机坐标系顶点集,即使用公式:\(P_c=RP_w+t\),求解步骤代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
# 定义一个角度
a = 45
# 转换为弧度制
a = np.deg2rad(a)
# 手动定一个相机外参R旋转矩阵,并设置让其绕roll轴旋转a度
R_roll = np.array([
[1, 0, 0],
[0, np.cos(a), -np.sin(a)],
[0, np.sin(a), np.cos(a)]
])
# 手动定一个相机外参的偏移向量t 即在x, y, z的位置看面朝单位
t1 = 0
t2 = 0
t3 = 5 # 数值越大则距离观测目标距离则越长
T = np.array([t1, t2, t3])
# 求基于相机坐标系的顶点集
vertices_c = np.matmul(R_roll, vertices_w.T).T + T
再求出新的点集后,我们手动定义一组相机内参的K矩阵,并将中心点设置在像素坐标系中画布的中心点,以便我们可视化时可能更清晰的观测到目标;定义内参K矩阵后,我们定义一个透视投影函数,用于将三维的坐标系投影到像素坐标系中,即公式:\(zP_{uv}=KP\),函数定义如下:
1
2
3
4
5
6
7
8
def perspective_projection(vertices, K):
"""use perspective projection"""
vertices_2d = np.matmul(K, vertices.T).T
vertices_2d[:, 0] /= vertices_2d[:, 2]
vertices_2d[:, 1] /= vertices_2d[:, 2]
vertices_2d = vertices_2d[:, :2].astype(np.int32)
return vertices_2d
定义好函数perspective_projection后,我们在主程序中继续定义我们的内参矩阵K,并使用函数进行坐标转换:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 手动定一组相机内参K
fx = 800
fy = 800
cx = canvas_square_size // 2
cy = canvas_square_size // 2
K = np.array([
[fx, 0, cx],
[0, fy, cy],
[0, 0, 1]
])
# 使用透视投影解出像素坐标的顶点集
vertices_uv = perspective_projection(vertices_c, K)
print("像素坐标系顶点集合: ", vertices_uv.shape)
# 打印结果:
# 世界坐标系顶点集合: (8, 3)
完成像素坐标系的转换后,我们准备一个绘制函数,用来显示我们的处理结果,将投影后的像素坐标系显示出来:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
def display_vertices_uv(vertices_2d, win_name='vertices', wait_key=0, canvas_size=(320, 320)):
"""Show the vertices on uv-coordinates"""
img = np.zeros((canvas_size[0], canvas_size[1], 3), dtype=np.uint8)
edges = np.array([
[0, 1], [0, 2], [0, 4],
[1, 3], [1, 5],
[2, 3], [2, 6],
[4, 5], [4, 6],
[7, 5], [7, 6], [7, 3]])
for edge in edges:
pt1 = tuple(vertices_2d[edge[0]])
pt2 = tuple(vertices_2d[edge[1]])
cv2.line(img, pt1, pt2, (0, 255, 255), 2)
cv2.imshow(win_name, img)
cv2.waitKey(wait_key)
定义好函数后,我们回到主程序运行代码显示结果:
1
2
# 显示求解后的uv顶点集
display_vertices_uv(vertices_uv, canvas_size=(canvas_square_size, canvas_square_size))
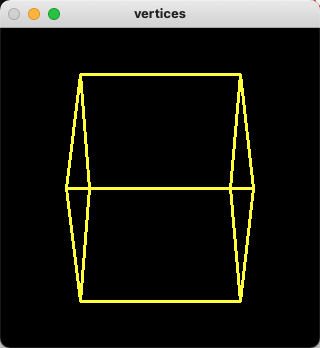
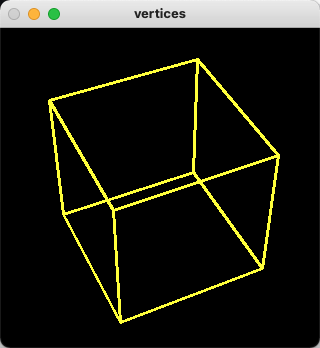
结果如下:
可以看到我们已经成功的使用自己定义的模拟相机内外参去对该立方体进行世界坐标转换到像素坐标,并成功可视化观测到这个立方体。 这里我们将相机通过外参矩阵R的形式设置的是把相机摆放在一个以roll转角45度的观测角度,为了以更加丰富的角度观测到这个立方体,我们可以在roll转角45度的情况下,再加入另外一种欧拉角属性pitch,使其可以添加一种新的角度去观测该对象,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
# 再定义一组旋转矩阵,以pitch轴进行b度旋转
b = 25
b = np.deg2rad(b)
R_pitch = np.array([
[0, np.cos(b), -np.sin(b)],
[1, 0, 0],
[0, np.sin(b), np.cos(b)]
])
# 重新调整一下外参的旋转矩阵R
R = np.matmul(R_roll, R_pitch)
# 重新求基于相机坐标系的顶点集 加入yaw旋转角
vertices_c_pitch = np.matmul(R, vertices_w.T).T + T
# 继续使用内参K透视投影解出像素坐标的顶点集
vertices_uv_pitch = perspective_projection(vertices_c_pitch, K)
# 显示求解后的uv顶点集
display_vertices_uv(vertices_uv_pitch)
通过代码可得知我们在重新定义了一个外参矩阵R,是将之前定义的外参矩阵R_roll与当前新定义的R_pitch进行一个线性变换处理所得出的结果,其目的是让机位角在roll轴旋转45度的情况下再对其pitch轴旋转25度,得出该外参矩阵并进行坐标转换,结果如下:
可以看到我们能观测到的立方体视角更加丰富了.
示例2:使用解PnP求出外参矩阵
通过上述的案例,我们手动定义了相机的内外参矩阵,这里补充一点,在知道观测目标的世界坐标与相机内参的情况下,我们是可以使用一些数学手段去解出相机的外参矩阵的,这里采用的方法是使用opencv提供的solvePnP解法,去解出外参矩阵,接续上一个案例下进行代码的补充即可,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
# 使用solvePnP尝试解出相机外参
rvec = np.zeros((3, 1))
tvec = np.zeros((3, 1))
retval, rvec, tvec = cv2.solvePnP(vertices_w.astype(np.float32), vertices_uv_pitch.astype(np.float32),
K.astype(np.float32),
None, rvec, tvec, False, cv2.SOLVEPNP_ITERATIVE)
R_solved, _ = cv2.Rodrigues(rvec)
print("解PnP得出的R Matrix: ", -R_solved) # 解出的坐标系是反着需要自行调整
print("自己定的R Matrix: ", R)
# 打印结果:
# 解PnP得出的R Matrix: [[ 1.27441147e-04 9.06220345e-01 -4.22805713e-01]
# [ 7.06805406e-01 -2.99177784e-01 -6.41029463e-01]
# [ 7.07408017e-01 2.98759670e-01 6.40559566e-01]]
# 自己定的R Matrix: [[ 0. 0.90630779 -0.42261826]
# [ 0.70710678 -0.29883624 -0.64085638]
# [ 0.70710678 0.29883624 0.64085638]]
可以看到,使用solvePnP解出的外参矩阵R与我们自行定义的矩阵R基本相等,该结果的精度与观测目标的顶点数量有关,顶点越多精度会越高。
示例3:旋转的立方体
通过上面的案例,我们可以写一个小玩意,通过不断的改变相机外参来实时更新并显示出被观测对象的画面,可让立方体仿佛动起来一样,代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
# 定义方形画布像素坐标长度
canvas_square_size = 320
# 定义立方体的边长
length = 1
# 定义立方体的8个顶点坐标
vertices_w = np.array([
[-length / 2, -length / 2, -length / 2],
[-length / 2, -length / 2, length / 2],
[-length / 2, length / 2, -length / 2],
[-length / 2, length / 2, length / 2],
[length / 2, -length / 2, -length / 2],
[length / 2, -length / 2, length / 2],
[length / 2, length / 2, -length / 2],
[length / 2, length / 2, length / 2]])
# 手动定一组相机内参K
fx = 800
fy = 800
cx = canvas_square_size // 2
cy = canvas_square_size // 2
K = np.array([
[fx, 0, cx],
[0, fy, cy],
[0, 0, 1]
])
# 初始化角度
a = 0
while True:
# 手动定一个相机外参R旋转矩阵,并设置让三个轴旋转a度
R = construct_extrinsic_matrix_R(a, a, a)
# 手动定一个相机外参的偏移向量t 即在x, y, z的位置看面朝单位
t1 = 0
t2 = 0
t3 = 5 # 数值越大则距离观测目标距离则越长
T = np.array([t1, t2, t3])
# 求基于相机坐标系的顶点集
vertices_c = np.matmul(R, vertices_w.T).T + T
# 使用透视投影解出像素坐标的顶点集
vertices_uv = perspective_projection(vertices_c, K)
# 显示求解后的uv顶点集
display_vertices_uv(vertices_uv, wait_key=30, canvas_size=(canvas_square_size, canvas_square_size))
a += 1
结果如下:
完整代码:
所有示例的完整代码如下:
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
import cv2
import numpy as np
def display_vertices_uv(vertices_2d, win_name='vertices', wait_key=0, canvas_size=(320, 320)):
"""Show the vertices on uv-coordinates"""
img = np.zeros((canvas_size[0], canvas_size[1], 3), dtype=np.uint8)
edges = np.array([
[0, 1], [0, 2], [0, 4],
[1, 3], [1, 5],
[2, 3], [2, 6],
[4, 5], [4, 6],
[7, 5], [7, 6], [7, 3]])
for edge in edges:
pt1 = tuple(vertices_2d[edge[0]])
pt2 = tuple(vertices_2d[edge[1]])
cv2.line(img, pt1, pt2, (0, 255, 255), 2)
cv2.imshow(win_name, img)
cv2.waitKey(wait_key)
def perspective_projection(vertices, K):
"""use perspective projection"""
vertices_2d = np.matmul(K, vertices.T).T
vertices_2d[:, 0] /= vertices_2d[:, 2]
vertices_2d[:, 1] /= vertices_2d[:, 2]
vertices_2d = vertices_2d[:, :2].astype(np.int32)
return vertices_2d
def construct_extrinsic_matrix_R(yaw_angle, roll_angle, pitch_angle):
"""Construct the camera external parameter rotation matrix R"""
yaw = np.deg2rad(yaw_angle)
roll = np.deg2rad(roll_angle)
pitch = np.deg2rad(pitch_angle)
R_yaw = np.array([
[np.cos(yaw), -np.sin(yaw), 0],
[np.sin(yaw), np.cos(yaw), 0],
[0, 0, 1]
])
R_roll = np.array([
[1, 0, 0],
[0, np.cos(roll), -np.sin(roll)],
[0, np.sin(roll), np.cos(roll)]
])
R_pitch = np.array([
[0, np.cos(pitch), -np.sin(pitch)],
[1, 0, 0],
[0, np.sin(pitch), np.cos(pitch)]
])
R = np.matmul(R_pitch, np.matmul(R_yaw, R_roll))
return R
def sample_a():
# 定义方形画布像素坐标长度
canvas_square_size = 320
# 定义立方体的边长
length = 1
# 定义立方体的8个顶点坐标 使用世界坐标作为表达
vertices_w = np.array([
[-length / 2, -length / 2, -length / 2],
[-length / 2, -length / 2, length / 2],
[-length / 2, length / 2, -length / 2],
[-length / 2, length / 2, length / 2],
[length / 2, -length / 2, -length / 2],
[length / 2, -length / 2, length / 2],
[length / 2, length / 2, -length / 2],
[length / 2, length / 2, length / 2]])
print("世界坐标系顶点集合: ", vertices_w.shape)
# 定义一个角度
a = 45
# 转换为弧度制
a = np.deg2rad(a)
# 手动定一个相机外参R旋转矩阵,并设置让其绕roll轴旋转a度
R_roll = np.array([
[1, 0, 0],
[0, np.cos(a), -np.sin(a)],
[0, np.sin(a), np.cos(a)]
])
# 手动定一个相机外参的偏移向量t 即在x, y, z的位置看面朝单位
t1 = 0
t2 = 0
t3 = 5 # 数值越大则距离观测目标距离则越长
T = np.array([t1, t2, t3])
# 求基于相机坐标系的顶点集
vertices_c = np.matmul(R_roll, vertices_w.T).T + T
# 手动定一组相机内参K
fx = 800
fy = 800
cx = canvas_square_size // 2
cy = canvas_square_size // 2
K = np.array([
[fx, 0, cx],
[0, fy, cy],
[0, 0, 1]
])
# 使用透视投影解出像素坐标的顶点集
vertices_uv = perspective_projection(vertices_c, K)
print("像素坐标系顶点集合: ", vertices_uv.shape)
# 显示求解后的uv顶点集
display_vertices_uv(vertices_uv, canvas_size=(canvas_square_size, canvas_square_size))
# 再定义一组旋转矩阵,以pitch轴进行b度旋转
b = 25
b = np.deg2rad(b)
R_pitch = np.array([
[0, np.cos(b), -np.sin(b)],
[1, 0, 0],
[0, np.sin(b), np.cos(b)]
])
# 重新调整一下外参的旋转矩阵R
R = np.matmul(R_roll, R_pitch)
# 重新求基于相机坐标系的顶点集 加入yaw旋转角
vertices_c_pitch = np.matmul(R, vertices_w.T).T + T
# 继续使用内参K透视投影解出像素坐标的顶点集
vertices_uv_pitch = perspective_projection(vertices_c_pitch, K)
# 显示求解后的uv顶点集
display_vertices_uv(vertices_uv_pitch)
# 使用solvePnP尝试解出相机外参
rvec = np.zeros((3, 1))
tvec = np.zeros((3, 1))
retval, rvec, tvec = cv2.solvePnP(vertices_w.astype(np.float32), vertices_uv_pitch.astype(np.float32),
K.astype(np.float32),
None, rvec, tvec, False, cv2.SOLVEPNP_ITERATIVE)
R_solved, _ = cv2.Rodrigues(rvec)
print("解PnP得出的R Matrix: ", -R_solved) # 解出的坐标系是反着需要自行调整
print("自己定的R Matrix: ", R)
def sample_b():
# 定义方形画布像素坐标长度
canvas_square_size = 320
# 定义立方体的边长
length = 1
# 定义立方体的8个顶点坐标
vertices_w = np.array([
[-length / 2, -length / 2, -length / 2],
[-length / 2, -length / 2, length / 2],
[-length / 2, length / 2, -length / 2],
[-length / 2, length / 2, length / 2],
[length / 2, -length / 2, -length / 2],
[length / 2, -length / 2, length / 2],
[length / 2, length / 2, -length / 2],
[length / 2, length / 2, length / 2]])
# 手动定一组相机内参K
fx = 800
fy = 800
cx = canvas_square_size // 2
cy = canvas_square_size // 2
K = np.array([
[fx, 0, cx],
[0, fy, cy],
[0, 0, 1]
])
# 初始化角度
a = 0
while True:
# 手动定一个相机外参R旋转矩阵,并设置让三个轴旋转a度
R = construct_extrinsic_matrix_R(a, a, a)
# 手动定一个相机外参的偏移向量t 即在x, y, z的位置看面朝单位
t1 = 0
t2 = 0
t3 = 5 # 数值越大则距离观测目标距离则越长
T = np.array([t1, t2, t3])
# 求基于相机坐标系的顶点集
vertices_c = np.matmul(R, vertices_w.T).T + T
# 使用透视投影解出像素坐标的顶点集
vertices_uv = perspective_projection(vertices_c, K)
# 显示求解后的uv顶点集
display_vertices_uv(vertices_uv, wait_key=30, canvas_size=(canvas_square_size, canvas_square_size))
a += 1
if __name__ == '__main__':
sample_a() # 示例1
sample_b() # 示例2
Note:
由于忘性较大,仓促实验和匆忙记录只为记录自己的理解和实验经过留后期继续学习和观看,可能会有不少理解错误,如果给您带来困扰烦请指正和海涵。